Multiple Choice
Graph the function using transformations.
- 
A) 
B) 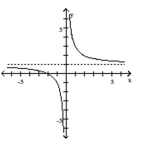
C) 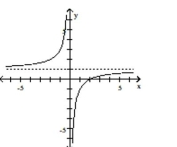
D) 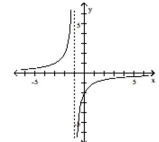
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q151: Solve the inequality.<br>- <span class="ql-formula" data-value="\frac
Q152: Write the word or phrase that
Q153: Write the word or phrase that
Q154: Give the equation of the horizontal
Q155: Information is given about a polynomial
Q157: Use the graph to find the
Q158: Solve the inequality.<br>- <span class="ql-formula" data-value="x
Q159: Information is given about a polynomial
Q160: Find the indicated intercept(s) of the
Q161: Write the word or phrase that