Multiple Choice
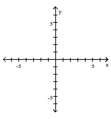
Graph the function using transformations.
- 
A) 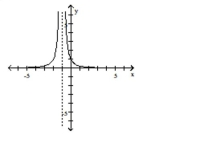
B) 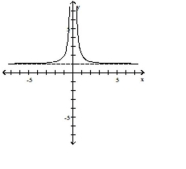
C) 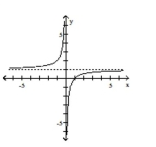
D) 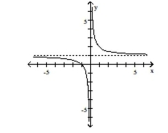
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q237: Write the word or phrase that
Q238: Solve the problem.<br>-Decide which of the
Q239: Find the x- and y-intercepts of
Q240: State whether the function is a
Q241: List the potential rational zeros of
Q243: Find all zeros of the function
Q244: Give the equation of the oblique
Q245: Choose the one alternative that best
Q246: Use transformations of the graph o
Q247: Find the indicated intercept(s) of the