Determine Whether the Graph Is That of a Function $\{x \mid-\pi \leq x \leq \pi\}$

Multiple Choice

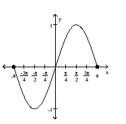
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if
any, and any symmetry with respect to the x-axis, the y-axis, or the origin.
-

A)
function
domain: $\{x \mid-\pi \leq x \leq \pi\}$
range: $\{y \mid-1 \leq y \leq 1\}$
intercepts: $(-\pi, 0) ,(0,0) ,(\pi, 0)$
symmetry: origin

B)
function
domain: all real numbers
range: $\{\mathrm{y} \mid-1 \leq \mathrm{y} \leq 1\}$
intercepts: $(-\pi, 0) ,(0,0) ,(\pi, 0)$
symmetry: origin

C)
function
domain: $\{x \mid-1 \leq x \leq 1\}$
range: $\{y \mid-\pi \leq y \leq \pi\}$
intercepts: $(-\pi, 0) ,(0,0) ,(\pi, 0)$
symmetry: none

D)
$\text { not a function }$