Multiple Choice
Graph the Polar Equations of Conics
- Identify the directrix and vertices.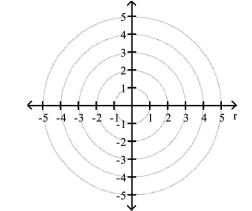
A) directrix: 2 unit(s) to the left of
the pole at
vertices: 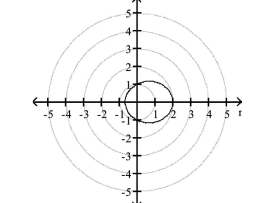
B) directrix: 2 unit(s) to the right of
the pole at
vertices: 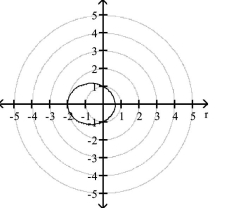
C) directrix: 2 unit(s) below
the pole at
vertices: 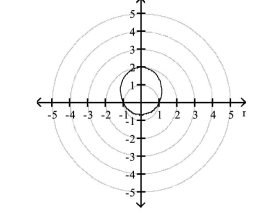
D) directrix: 2 unit(s) above
the pole at
vertices: 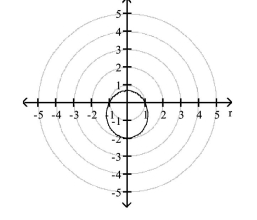
Correct Answer:

Verified
Correct Answer:
Verified
Q152: Additional Concepts<br>- <span class="ql-formula" data-value="\frac {
Q153: Solve Apps: Conic Sections in Polar
Q154: Additional Concepts<br>- <span class="ql-formula" data-value="\frac {
Q155: Tech: Rotation of Axes<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7044/.jpg" alt="Tech: Rotation
Q156: Parametric Equations<br>1 Use Point Plotting to
Q158: Write Equations of Rotated Conics in
Q159: Find the solution set for the
Q160: Graph the parabola with the given
Q161: Solve Applied Problems Involving Parabolas<br>-A reflecting
Q162: Sketch the function represented by the