Multiple Choice
Graph the Polar Equations of Conics
- Identify the directrix and vertices.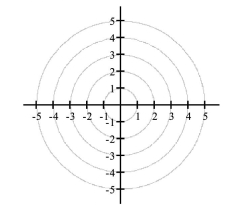
A) directrix: unit(s) abovethe pole at
vertices: 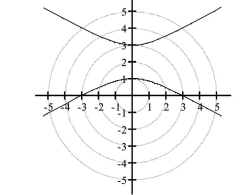
B) directrix: unit(s) below
the pole at
vertices: 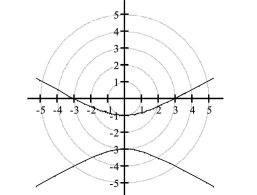
C) directrix: unit(s) to the left ofthe pole at
vertices: 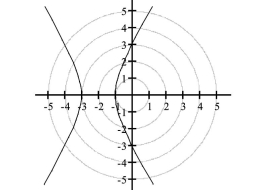
D) directrix: unit(s) to the right of
the pole at
vertices: 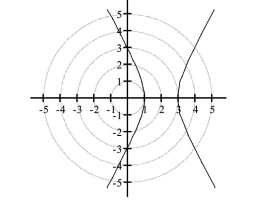
Correct Answer:

Verified
Correct Answer:
Verified
Q113: Additional Concepts<br>- <span class="ql-formula" data-value="y =
Q114: Convert the equation to the standard
Q115: Find the standard form of the
Q116: Find Parametric Equations for Functions<br>-The line
Q117: Additional Concepts<br>- <span class="ql-formula" data-value="y ^
Q119: Eliminate the Parameter<br>-A circle: <span
Q120: Graph the Polar Equations of Conics<br>-
Q121: Rotation of Axes<br>1 Identify Conics Without
Q122: Convert the equation to the standard
Q123: Use point plotting to graph the