Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of .
A) 
B) 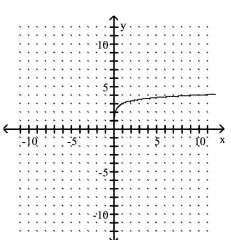
C) 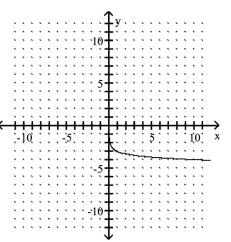
D) 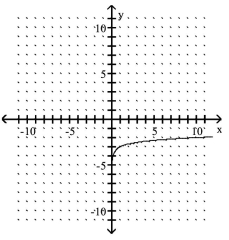
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q259: Solve the problem.<br>-Find out how long
Q260: Use properties of logarithms to condense
Q261: Approximate the number using a calculator.
Q262: Use properties of logarithms to expand
Q263: Use properties of logarithms to expand
Q265: Use properties of logarithms to condense
Q266: Use the compound interest formulas A
Q267: Choose the one alternative that best
Q268: Use common logarithms or natural logarithms
Q269: The graph of a logarithmic function