Related Questions
Q67: Find the domain and range of
Q68: Find the horizontal asymptote, if any,
Q69: Determine the maximum possible number of
Q70: Determine whether the function is a
Q71: Use synthetic division and the Remainder
Q73: Find the y-intercept of the polynomial
Q74: Find the coordinates of the vertex
Q75: Solve Combined Variation Problems<br>- <span class="ql-formula"
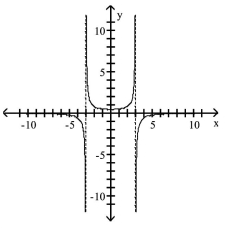
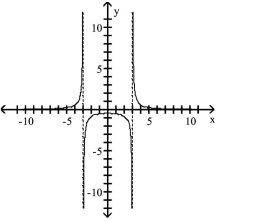
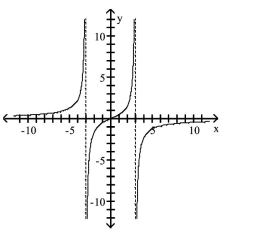
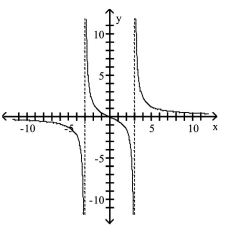
Q76: Graph the rational function.<br>- <span class="ql-formula"
Q77: Divide using synthetic division.<br>- <span class="ql-formula"