Solved

Choose the One Alternative That Best Completes the Statement or Answers

Question 170

Multiple Choice

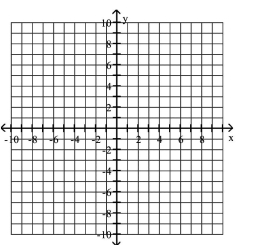
Choose the one alternative that best completes the statement or answers the question. Graph ff as a solid line and f−1\mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of ff and f−1f ^ { - 1 } .
- f(x) =x2−1,x≥0f ( x ) = x ^ { 2 } - 1 , x \geq 0
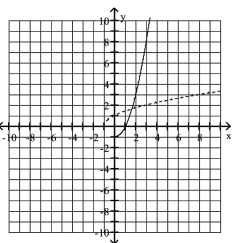
Choose the one alternative that best completes the statement or answers the question. Graph f as a solid line and \mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of f and f ^ { - 1 } . - f ( x ) = x ^ { 2 } - 1 , x \geq 0 A) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) B) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) C) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( 1 , \infty ) D) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( 1 , \infty )


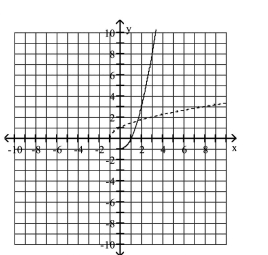
A) Choose the one alternative that best completes the statement or answers the question. Graph f as a solid line and \mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of f and f ^ { - 1 } . - f ( x ) = x ^ { 2 } - 1 , x \geq 0 A) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) B) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) C) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( 1 , \infty ) D) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( 1 , \infty )
ff domain =(0,∞) = ( 0 , \infty ) ; range =(−1,∞) = ( - 1 , \infty )
f−1f ^ { - 1 } domain =(0,∞) = ( 0 , \infty ) ; range =(−1,∞) = ( - 1 , \infty )

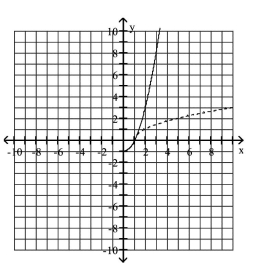
B) Choose the one alternative that best completes the statement or answers the question. Graph f as a solid line and \mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of f and f ^ { - 1 } . - f ( x ) = x ^ { 2 } - 1 , x \geq 0 A) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) B) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) C) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( 1 , \infty ) D) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( 1 , \infty )
ff domain =(−∞,∞) = ( - \infty , \infty ) ; range =(−1,∞) = ( - 1 , \infty )
f−1f ^ { - 1 } domain =(−∞,∞) = ( - \infty , \infty ) ; range =(−1,∞) = ( - 1 , \infty )


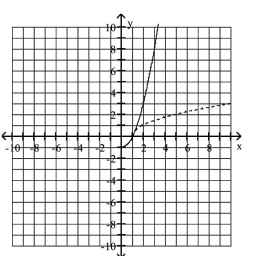
C) Choose the one alternative that best completes the statement or answers the question. Graph f as a solid line and \mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of f and f ^ { - 1 } . - f ( x ) = x ^ { 2 } - 1 , x \geq 0 A) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) B) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) C) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( 1 , \infty ) D) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( 1 , \infty )
ff domain =(0,∞) = ( 0 , \infty ) ; range =(−1,∞) = ( - 1 , \infty )
f−1f ^ { - 1 } domain =(0,∞) = ( 0 , \infty ) ; range =(1,∞) = ( 1 , \infty )

D) Choose the one alternative that best completes the statement or answers the question. Graph f as a solid line and \mathrm { f } ^ { - 1 } as a dashed line in the same rectangular coordinate space. Use interval notation to give the domain and range of f and f ^ { - 1 } . - f ( x ) = x ^ { 2 } - 1 , x \geq 0 A) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) B) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) C) f domain = ( 0 , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( 0 , \infty ) ; range = ( 1 , \infty ) D) f domain = ( - \infty , \infty ) ; range = ( - 1 , \infty ) f ^ { - 1 } domain = ( - \infty , \infty ) ; range = ( 1 , \infty )
ff domain =(−∞,∞) = ( - \infty , \infty ) ; range =(−1,∞) = ( - 1 , \infty )
f−1f ^ { - 1 } domain =(−∞,∞) = ( - \infty , \infty ) ; range =(1,∞) = ( 1 , \infty )

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q165: Identify the Domain and Range of

Q166: Give the domain and range of

Q167: Find functions f and g so

Q168: Given functions f and g, perform

Q169: Begin by graphing the standard quadratic

Q171: Begin by graphing the standard cube

Q172: Find the domain of the function.<br>-

Q173: Given functions f and g, perform

Q174: For the given functions f and

Q175: Choose the one alternative that best