Related Questions
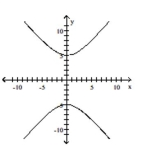
Q144: Write an equation for the parabola.<br>-vertex
Q145: Match the equation of the ellipse
Q146: What is the probability that the
Q147: If an object is thrown upward with
Q148: Write an equation for the parabola.<br>-vertex:
Q150: Write the binomial expansion of the
Q151: Use the formula for S<sub>n</sub> to
Q152: Write out the first five terms
Q153: Graph the ellipse.<br>- <span class="ql-formula" data-value="4(x+1)^{2}+9(y+2)^{2}=36"><span
Q154: The roof of a building is