Essay
To graph on a graphics calculator, we must consider the union of the graphs of the two functions, and . Using the graph of , explain (a) how the solution set of can be determined graphically and (b) how it relates to the domain of the hyperbola.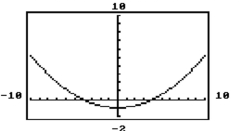
Correct Answer:

Verified
The graph of  lies above or on...
lies above or on...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q199: Write an equation for the parabola.<br>-vertex
Q200: Provide an appropriate response.<br>-Consider determining how many
Q201: Evaluate the expression.<br>- <span class="ql-formula" data-value="\frac
Q202: A sequence of yearly payments of $5000
Q203: Find the first term and the
Q205: Find the sum of the first
Q206: Martin saves $5 on the first day
Q207: In how many ways can 8 people
Q208: Write an equation for the parabola
Q209: Write an equation for the hyperbola.<br>-vertices