Multiple Choice
For the function as defined that is one-to-one, graph f and on the same axes.
- 
A) 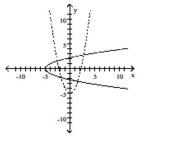
B) 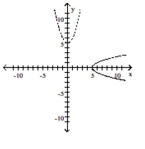
C) 
D) not one-to-one
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q462: For the function as defined that
Q463: Give the answer in exact form.<br>-
Q464: Find the number of years for $14,100
Q465: Find the function value. If the
Q466: Solve for the indicated variable.<br>- <span
Q467: Determine whether or not the function
Q469: Write in logarithmic form.<br>- <span class="ql-formula"
Q470: Use properties of logarithms to evaluate
Q471: Solve the equation and express the
Q472: Write an equivalent expression in exponential