Multiple Choice
For the function as defined that is one-to-one, graph f and on the same axes.
- 
A) 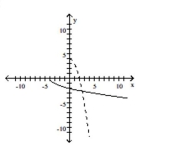
B) 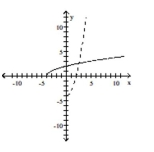
C) 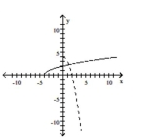
D) 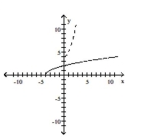
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q134: Use the definition of inverses to
Q135: Match the function with its graph.<br>-
Q136: Solve for the indicated variable.<br>- <span
Q137: Determine whether or not the function is
Q138: Write an equation for the graph
Q140: Write an equation for the graph
Q141: Find the future value.<br>-$3622 invested for 11
Q142: Provide an appropriate response.<br>-Why can'
Q143: A lake is stocked with 422
Q144: If the function is one-to-one, find