Multiple Choice
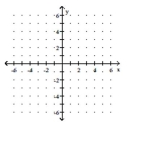
Give the domain and range.
- 
A) domain: ; range: 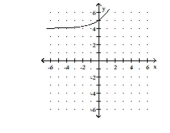
B) domain: ; range: 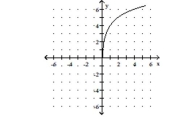
C) domain: ; range: 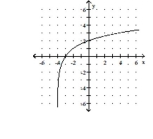
D) domain: ; range: 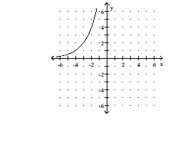
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q356: The hydrogen potential, <span class="ql-formula"
Q357: Graph the exponential function using transformations where
Q358: Decide whether the given functions are
Q359: Determine whether or not the function
Q360: Determine whether the statement is true
Q362: Find the value. Give an approximation
Q363: What are the domain and range
Q364: Give the domain and range.<br>- <span
Q365: Determine whether or not the function
Q366: Use the properties of logarithms to