Multiple Choice
Find a polynomial function f(x) of least possible degree having the graph shown.
-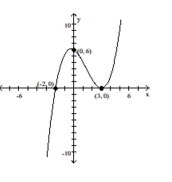
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q471: Determine whether the statement is true
Q472: Find the correct end behavior diagram
Q473: Solve the inequality. Write the solution
Q474: Give the equations of any horizontal
Q475: Use synthetic division to decide whether
Q477: Solve the problem. Round your answer to
Q478: Provide an appropriate response.<br>-For what value
Q479: Graph the polynomial function. Factor first
Q480: A toy rocket is shot vertically
Q481: Identify the vertex of the parabola.<br>-