Multiple Choice
Determine whether the statement is true or false.
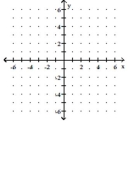
- 
A) 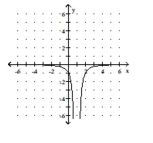
B) 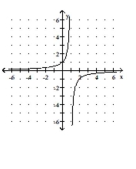
C) 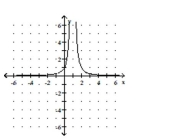
D) 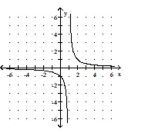
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q71: The graph of <span class="ql-formula"
Q72: Sketch the graph of the parabola.<br>-
Q73: Tell whether a linear model or
Q74: How can the graph of
Q75: Use synthetic division to decide whether
Q77: The graph of <span class="ql-formula"
Q78: Use a graphing calculator to find
Q79: Sketch the graph of the parabola.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7516/.jpg"
Q80: Find a quadratic function f having
Q81: A ball is tossed upward. Its