Multiple Choice
Sketch the graph of the rational function.
- 
A) 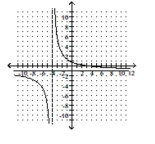
B) 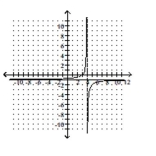
C) 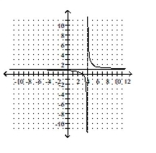
D) 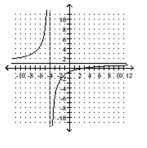
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q493: Round to the nearest tenth unless indicated
Q494: Find a polynomial of degree 3
Q495: The polynomial function <span class="ql-formula"
Q496: Tell whether a linear model or
Q497: Use synthetic division to decide whether
Q499: Use the factor theorem to decide
Q500: Find a polynomial of degree 3
Q501: Give the equations of any vertical
Q502: Use the intermediate value theorem for
Q503: Use the remainder theorem and synthetic