Multiple Choice
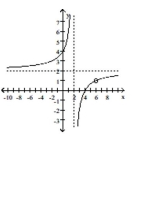
Find an equation for the rational function graph.
-
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q381: Use synthetic division <span class="ql-formula"
Q382: Identify the vertex of the parabola.<br>-Identify
Q383: Sketch the graph of the polynomial function.<br>-<img
Q384: Determine which of the rational functions
Q385: Use the equation and the corresponding
Q387: Find an equation for the rational
Q388: Use the graph to answer the
Q389: If the average cost per unit C(x)
Q390: Suppose the cost per ton,
Q391: Find the zeros of the polynomial