Multiple Choice
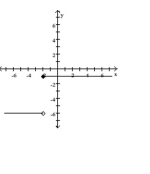
Give a rule for the piecewise-defined function. Then give the domain and range.
-
A)
B) Domain: , Range:
C) Domain: , Range:
D) Domain: , Range:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q416: Decide whether or not the equation
Q417: Graph the point symmetric to the
Q418: Determine the intervals of the domain
Q419: Find the specified domain.<br>-Find the domain
Q420: Consider the function h as defined.
Q422: Decide whether the relation defines a function.<br>-<img
Q423: Match the equation with the correct
Q424: Graph the linear function and give
Q425: The graph of y = f(x)
Q426: Determine whether the equation has a