Multiple Choice
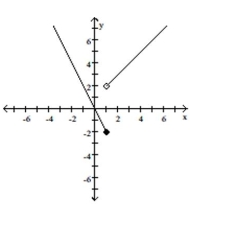
Give a rule for the piecewise-defined function. Then give the domain and range.
-
A) Domain: , Range:
B) Domain: , Range:
C) Domain: , Range:
D) Domain: , Range:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q324: Match the equation with the correct
Q325: Graph the circle.<br>- <span class="ql-formula" data-value="(x-1)^{2}+(y+3)^{2}=25"><span
Q326: Find the slope of the line
Q327: Give the domain and range of
Q328: Find the requested value.<br>- <span class="ql-formula"
Q330: Match the equation with the correct
Q331: Determine whether the three points are
Q332: Write an equation for the line
Q333: Write an equation for the line
Q334: Find the center-radius form of the