Describe the Transformations and Give the Equation for the Graph $f ( x ) = \sqrt { x }$

Multiple Choice

Describe the transformations and give the equation for the graph.
-

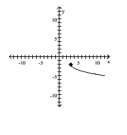
A) It is the graph of $f ( x ) = \sqrt { x }$ translated 3 units to the right, reflected across the $y$ -axis and translated 2 units down. The equation is $y = \sqrt { - x - 3 } - 2$
B) It is the graph of $f ( x ) = \sqrt { x }$ translated 3 units to the right, reflected across the $x$ -axis and translated 2 units down. The equation is $y = \sqrt { - x + 3 } - 2$
C) It is the graph of $f ( x ) = \sqrt { x }$ translated 3 units to the right, reflected across the $x$ -axis and translated 2 units down. The equation is $y = - \sqrt { x + 3 } - 2$
D) It is the graph of $f ( x ) = \sqrt { x }$ translated 3 units to the right, reflected across the $x$ -axis and translated 2 units down. The equation is $y = - \sqrt { x - 3 } - 2$