Essay
Provide the requested proof.
-In the trapezoid below, and . If is the midpoint of , prove that .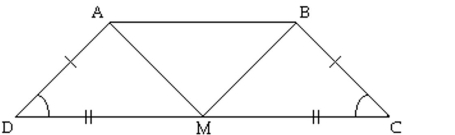
Correct Answer:

Verified
Answers will vary. A sample co...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q99: Solve.<br>-Explain how to construct a square
Q100: Solve.<br>-Inscribe a circle into a square.
Q101: Solve.<br>-Explain how to construct a line parallel
Q102: These triangles are similar. Find the
Q103: Provide an appropriate response.<br>-Use the fact
Q105: The perpendicular bisectors of a triangle are
Q106: Solve.<br>-Given two 15-cm sides and two 10-cm
Q107: Answer the question.<br>-Can a parallelogram have exactly
Q108: Answer the question.<br>-Are two parallelograms always similar?
Q109: Answer the question.<br>-A rectangle is a trapezoid.