Multiple Choice
Use the properties of parallel lines to solve the problem.
-If and , what are the measures of the other angles?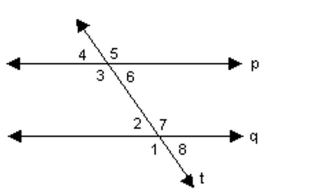
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q59: Decide whether the figure is convex or
Q60: Find the measure of the dihedral
Q61: Identify the triangle as scalene, isosceles, or
Q62: Refer to this figure to answer
Q63: Refer to this figure to answer
Q65: Find the requested angle.<br>-Supplement of 45°<br>A)90°<br>B)315°<br>C)135°<br>D)45°
Q66: Complete the sketch so that it has
Q67: Tell whether the angle is acute, right,
Q68: Determine the measure of the interior
Q69: Solve the problem.<br>-Which of the lines in