Multiple Choice
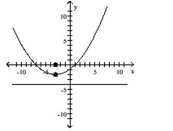
Find the vertex, focus, and directrix of the parabola. Graph the equation.
- 
A)
vertex:
focus:
directrix: 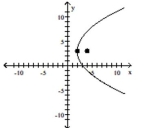
B)
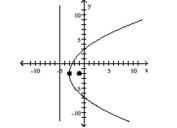
C)
vertex:
focus:
directrix: 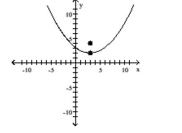
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q166: Graph the hyperbola.<br>- <span class="ql-formula" data-value="(y+1)^{2}-9(x-2)^{2}=9"><span
Q167: Find a rectangular equation for the
Q168: Find a polar equation for the
Q169: Graph the hyperbola.<br>- <span class="ql-formula" data-value="25
Q170: Rotate the axes so that the
Q172: Convert the polar equation to a
Q173: Name the conic.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7697/.jpg" alt="Name the conic.
Q174: Find an equation for the hyperbola
Q175: Write an equation for the parabola.<br>-<img
Q176: Rotate the axes so that the