Multiple Choice
Find the vertex, focus, and directrix of the parabola. Graph the equation.
- 
A)
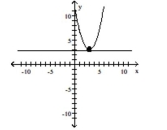
B)
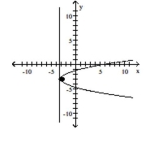
C)
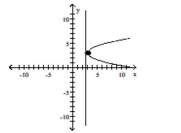
D)
vertex:
focus:
directrix: 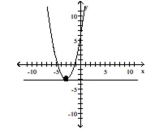
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q187: Find parametric equations for the rectangular
Q188: Find an equation for the ellipse
Q189: Rotate the axes so that the
Q190: Solve the problem.<br>-A reflecting telescope has
Q191: Find an equation of the parabola
Q193: Graph the hyperbola.<br>-The roof of a
Q194: Find the center, foci, and vertices
Q195: Find the vertex, focus, and directrix
Q196: Rotate the axes so that the
Q197: Graph the curve whose parametric equations