Multiple Choice
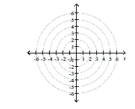
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
- 
A) 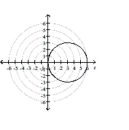
circle, radius 3 center at in rectangular coordinates
B) 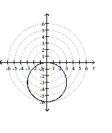
circle, radius 3
center at in rectangular coordinates
C) 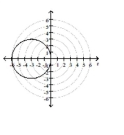
; circle, radius 3 ,
center at in rectangular coordinates
D) 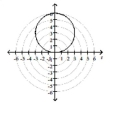
; circle, radius 3 ,
center at in rectangular coordinates
Correct Answer:

Verified
Correct Answer:
Verified
Q76: Use the figure below. Determine whether the
Q198: Use the vectors in the figure
Q199: The polar coordinates of a point
Q200: The polar coordinates of a point
Q201: Graph the polar equation.<br>- <span class="ql-formula"
Q202: Write the expression in the standard
Q204: Write the expression in the standard
Q205: Graph the polar equation.<br>- <span class="ql-formula"
Q207: Test the equation for symmetry with
Q208: Find the area of the parallelogram.<br>-