Multiple Choice
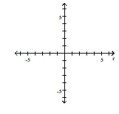
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
- 
A) 
; line through the pole making
an angle of with the polar axis
B) 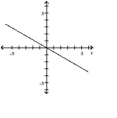
; line through the pole making
an angle of with the polar axis
C) 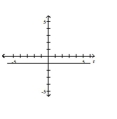
; horizontal line units
below the pole
D) 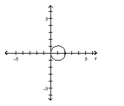
circle, radius
center at in rectangular coordinates
Correct Answer:

Verified
Correct Answer:
Verified
Q259: Find the value of the determinant.<br>-
Q260: Find the position vector for the vector
Q261: Match the graph to one of
Q262: Find the requested vector.<br>-v = -4i -
Q263: Find the indicated cross product.<br>-v = 4i
Q265: Find all the complex roots. Leave
Q266: The letters x and y represent
Q267: Find the area of the parallelogram.<br>-
Q268: Find the value of the determinant.<br>-
Q269: Plot the point given in polar