Multiple Choice
Use the method of adding y-coordinates to graph the function.
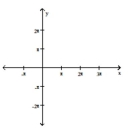
- 
A) 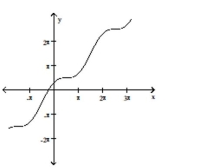
B) 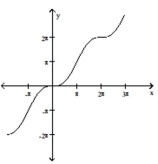
C) 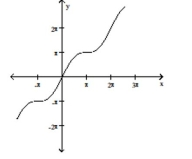
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q22: Solve the problem.<br>-The distance from home plate
Q37: Solve the problem.<br>-Two hikers on opposite sides
Q38: The displacement d (in meters) of
Q39: Find the area of the triangle. If
Q40: Solve the triangle.<br>- <span class="ql-formula" data-value="\beta
Q41: the motion is simple harmonic with
Q43: Find the area of the triangle.
Q44: Two sides of a right triangle
Q46: Two sides and an angle are
Q47: Solve the problem.<br>- <span class="ql-formula" data-value="\mathrm