Multiple Choice
Use the method of adding y-coordinates to graph the function.
- 
A) 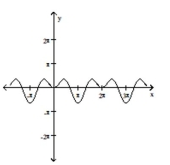
B) 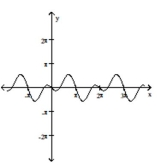 C)
C) 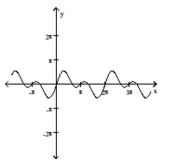
D) 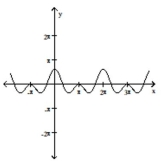
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q46: Two sides and an angle are
Q47: Solve the problem.<br>- <span class="ql-formula" data-value="\mathrm
Q49: Two sides of a right triangle
Q50: Solve the problem.<br>-A rocket tracking station has
Q52: Two sides of a right triangle
Q53: Solve the problem.<br>-A surveyor standing 56 meters
Q54: Solve the problem.<br>-Two surveyors 180 meters apart
Q56: Solve the triangle. Find the angles
Q70: Choose the one alternative that best completes
Q85: Solve the problem.<br>-A photographer points a camera