Essay
Solve the problem.
-When light travels from one medium to another-from air to water, for instance-it changes direction. (This is why a pencil, partially submerged in water, looks as though it is bent.) The angle of incidence is the angle in the first medium; the angle of refraction is the second medium. (See illustration.) Each medium has an index of refraction and , respectively -which can be found in tables. Snell's law relates these quantities in the forr
Solving for , we obtain
Find for air , methylene iodide , and .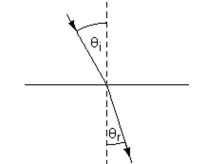
Correct Answer:

Verified
Correct Answer:
Verified
Q243: Complete the identity.<br>- <span class="ql-formula" data-value="\tan
Q244: Solve the problem using Snell's Law:
Q245: Find the exact value under the
Q246: Solve the problem.<br>-The average daily temperature
Q247: Use a calculator to solve the
Q249: Establish the identity.<br>- <span class="ql-formula" data-value="\frac
Q250: Solve the equation on the interval
Q251: Find the inverse function <span
Q252: Use the Half-angle Formulas to find
Q253: Solve the problem.<br>-When light travels from