Solve the Problem $$\mathrm { S } = \mathrm { kd } ^ { 3 } \sin ^ { 2 } \theta \cos \theta$$

Short Answer

Solve the problem.
-The strength S of a wooden beam with rectangular cross section is given by the formula $$\mathrm { S } = \mathrm { kd } ^ { 3 } \sin ^ { 2 } \theta \cos \theta$$ where d is the diagonal length, $$\theta$$ the angle illustrated, and k is a constant that varies with the type of wood used. 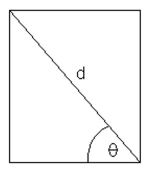Let $\mathrm { d } = 1$ and express the strength $\mathrm { S }$ in terms of the constant $\mathrm { k }$ for $\theta = 45 ^ { \circ } , 50 ^ { \circ } , 55 ^ { \circ } , 60 ^ { \circ }$ , and $65 ^ { \circ }$ . Does the strength always increase as $\theta$ gets larger?