Multiple Choice
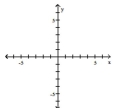
Graph the function using transformations.
- 
A) 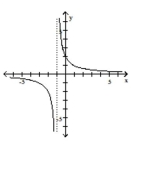
B) 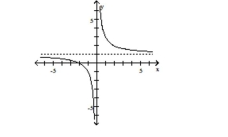
C) 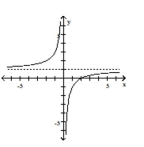
D) 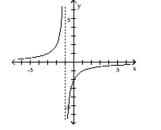
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q108: Solve the problem.<br>- <span class="ql-formula" data-value="x
Q109: Find the vertical asymptotes of the
Q110: State whether the function is a
Q111: For the polynomial, list each real
Q112: Find the x- and y-intercepts of
Q114: Use Descartes' Rule of Signs and
Q115: Graph the function using transformations.<br>- <span
Q116: Give the equation of the horizontal
Q117: Use the Factor Theorem to determine
Q118: The equation has a solution r