Multiple Choice
Graph the function using transformations.
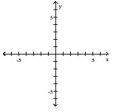
- 
A) 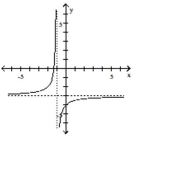
B) 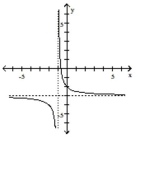
C) 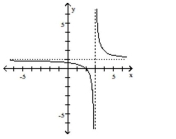
D) 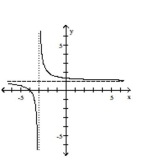
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q36: Solve the problem.<br>- <span class="ql-formula" data-value="x
Q37: List the potential rational zeros of
Q38: Find the domain of the rational
Q39: Find the indicated intercept(s) of the
Q40: State whether the function is a
Q42: Find the indicated intercept(s) of the
Q43: Find the x- and y-intercepts of
Q44: Form a polynomial whose zeros and
Q45: Use the graph to determine the
Q46: Use transformations of the graph o