Find and Simplify the Difference Quotient of F $$\frac { f ( x + h ) - f ( x ) } { h }$$

Multiple Choice

Find and simplify the difference quotient of f, $$\frac { f ( x + h ) - f ( x ) } { h }$$ $\mathbf { h } \neq 0$ , for the function.
- A)
function
domain: all real numbers
range: \( \{y \mid y \leq-2 \) or \( y \geq 2\} \)
intercepts: \( (-2,0) ,(2,0) \)
symmetry: \( y \) -axis\[\begin{array} { l l }

B)
function
domain: \( \{x \mid-2 \leq x \leq 2\} \)
range: all real numbers
intercepts: \( (-2,0) ,(2,0) \)
symmetry: \( \mathrm{x} \) -axis, \( y \) -axis

C)
function
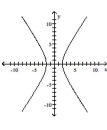
domain: \( \{x \mid x \leq-2 \) or \( x \geq 2\} \)
range: all real numbers
intercepts: \( (-2,0) ,(2,0) \)
symmetry: \( \mathrm{x} \) -axis, \( \mathrm{y} \) -axis, origirn

D)
\(\text { not a function }\)