Find and Simplify the Difference Quotient of F $$\frac { f ( x + h ) - f ( x ) } { h }$$

Multiple Choice

Find and simplify the difference quotient of f, $$\frac { f ( x + h ) - f ( x ) } { h }$$ $\mathbf { h } \neq 0$ , for the function.
- A)
$\begin{array}{l}\text { function } \\\text { domain: }\{x \mid-\pi \leq x \leq \pi\} \\\text { range: }\{y \mid-1 \leq y \leq 1\} \\\text { intercepts: }(-\pi, 0) ,(0,0) ,(\pi, 0) \\\text { symmetry: origin }\end{array}$


B)
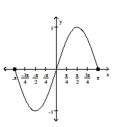
function
domain: all real numbers
range: $\{y \mid-1 \leq y \leq 1\}$
intercepts: $(-\pi, 0) ,(0,0) ,(\pi, 0)$
symmetry: origin

C)
function
domain: $\{x \mid-1 \leq x \leq 1\}$
range: $\{y \mid-\pi \leq y \leq \pi\}$
intercepts: $(-\pi, 0) ,(0,0) ,(\pi, 0)$
symmetry: none

D) not function