Multiple Choice
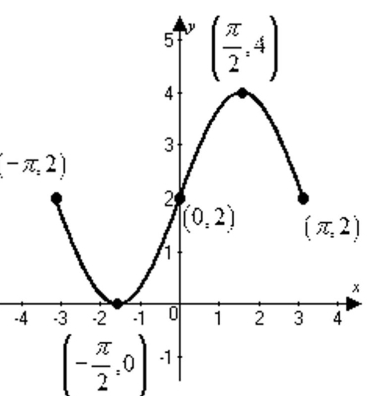
Use the graph to find the intervals on which it is increasing, decreasing, or constant.
-
A) Increasing on
B) Increasing on and ; decreasing on
C) Decreasing on and ; increasing on
D) Decreasing on ; increasing on
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q116: For the graph of the function
Q117: Answer the question about the given
Q118: The graph of a function is given.
Q119: Solve the problem.<br>-The price <span
Q121: The graph of a function is given.
Q122: Answer the question about the given
Q123: The graph of a function f
Q125: Find and simplify the difference quotient
Q167: Solve the problem.<br>-Two boats leave a dock
Q222: Solve the problem.<br>-A wire 20 feet long