Multiple Choice
The graph of a piecewise-defined function is given. Write a definition for the function.
-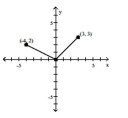 A)
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q231: Solve.<br>-The amount of paint needed to cover
Q260: For the given functions f and
Q261: Graph the function.<br>- <span class="ql-formula" data-value="f
Q262: Match the graph to the function listed
Q263: Graph the function.<br>- <span class="ql-formula" data-value="f(x)=\left\{\begin{array}{ll}-x+3
Q264: Locate any intercepts of the function.<br>-
Q266: Find and simplify the difference quotient
Q267: For the function, find the average
Q268: Write the word or phrase that
Q269: Choose the one alternative that best