Multiple Choice
Graph the exponential function using transformations where appropriate.
- 
A) 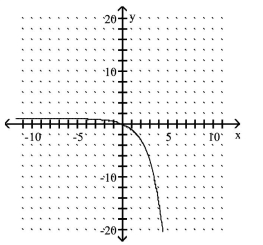
B) 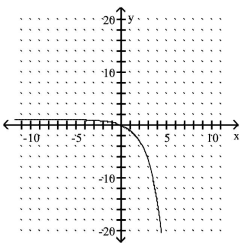
C) 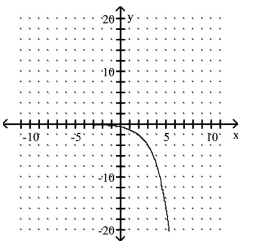
D) 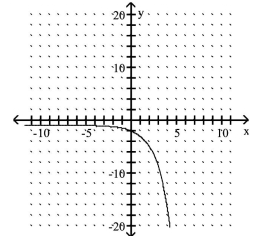
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q378: Use the change of base rule
Q379: Determine the function value.<br>-Suppose f(x) = logax
Q380: Write the word or phrase that
Q381: Solve the problem.<br>-The number of reports of
Q382: Decide whether or not the functions
Q384: Write the word or phrase that
Q385: Decide whether the given functions are
Q386: Find the function value. If the
Q387: Write an equivalent expression in exponential
Q388: Given <span class="ql-formula" data-value="\log _