Multiple Choice
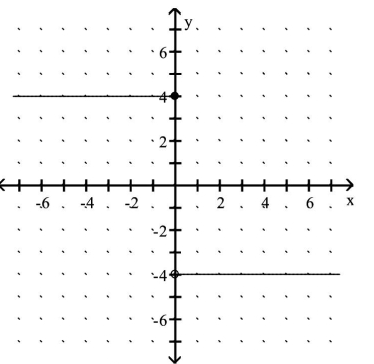
Give a rule for the piecewise-defined function. Then give the domain and range.
-
A) Domain: , Range:
B) ; Domain: , Range:
C) Domain: , Range:
D) ; Domain: , Range:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q502: Find the center-radius form of the
Q503: Suppose the point (2, 4) is on
Q504: Write an equation for the line
Q505: Decide whether the relation defines a
Q506: Use the graph to determine the
Q508: Decide whether the relation defines a
Q509: Give a rule for the piecewise-defined
Q510: Solve the problem.<br>-Use the graphs to
Q511: Give the domain and range of
Q512: Solve the problem.<br>-Find the center-radius form