Multiple Choice
Describe the transformations and give the equation for the graph.
-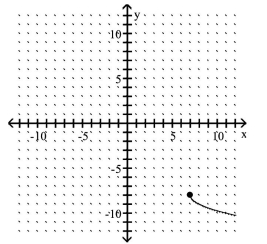
A) It is the graph of translated 7 units to the right, reflected across the -axis and translated 8 units down. The equation is
B) It is the graph of translated 7 units to the right, reflected across the -axis and translated 8 units down. The equation is
C) It is the graph of translated 7 units to the right, reflected across the -axis and translated 8 units down. The equation is
D) It is the graph of translated 7 units to the right, reflected across the -axis and translated 8 units down. The equation is
Correct Answer:

Verified
Correct Answer:
Verified
Q277: Decide whether the relation defines a function.<br>-<img
Q278: For the points P and Q,
Q279: Graph the line and give the
Q280: The graph of a linear function
Q281: Determine the intervals of the domain
Q283: Solve the problem.<br>-A furniture store buys 40
Q284: Find the slope and the y-intercept
Q285: Match the description with the correct symbolic
Q286: Decide whether or not the equation
Q287: Determine if the function is even,