Multiple Choice
Describe the transformations and give the equation for the graph.
-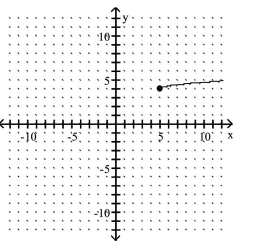
A) It is the graph of translated 5 units to the right, shrunken vertically by a factor of and translated 4 units up. The equation is
B) It is the graph of translated 5 units to the right, shrunken vertically by a factor of and translated 4 units up. The equation is
C) It is the graph of translated 5 units to the right, stretched vertically by a factor of 3 and translated 4 units up. The equation is
D) It is the graph of translated 5 units to the right, stretched vertically by a factor of 3 and translated 4 units up. The equation is
Correct Answer:

Verified
Correct Answer:
Verified
Q178: Solve the problem.<br>-The charges for renting
Q179: Solve the problem. Write all linear
Q180: Decide whether the relation defines a function.<br>-<img
Q181: Evaluate the function.<br>-Find <span class="ql-formula"
Q182: Write an equation for the line
Q184: Solve the problem.<br>-Select the equation that
Q185: Solve the problem.<br>-Employees of a publishing company
Q186: Graph the function.<br>- <span class="ql-formula" data-value="f
Q187: Give the domain and range of
Q188: Evaluate.<br>-Find <span class="ql-formula" data-value="\left( \frac