Multiple Choice
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
- 
A) center ; radius 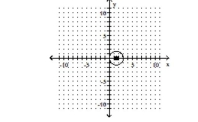
B) center radius 
C) center ; radius 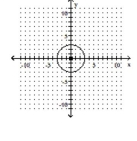
D) center ; radius 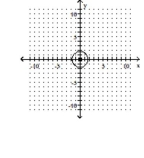
Correct Answer:

Verified
Correct Answer:
Verified
Q88: Sketch the graph of the equation.
Q89: Solve the system.<br>- <span class="ql-formula" data-value="\left\{
Q90: Graph the inequality.<br>- <span class="ql-formula" data-value="\frac{x^{2}}{4}+\frac{y^{2}}{16}
Q91: Solve the nonlinear system of equations
Q92: Solve the nonlinear system of equations
Q94: Graph the inequality.<br>- <span class="ql-formula" data-value="\frac
Q95: Solve.<br>-Comet's orbit the Sun in elongated
Q96: Graph the system.<br>- <span class="ql-formula" data-value="\left\{
Q97: Solve the nonlinear system of equations
Q98: Sketch the graph of the equation.