Multiple Choice
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
- 
A) center ; radius 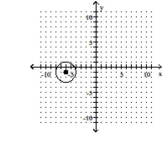
B) center ; radius 
C) center ; radius 
D) center ; radius 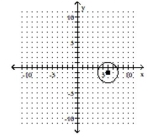
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q46: Sketch the graph of the equation.
Q47: Sketch the graph of the equation.
Q48: The graph of the equation is
Q49: Fill in the blank with one
Q50: Solve the nonlinear system of equations
Q52: Fill in the blank with one
Q53: Graph the equation.<br>- <span class="ql-formula" data-value="\frac
Q54: The graph of the equation is
Q55: Graph the equation.<br>- <span class="ql-formula" data-value="\frac
Q56: Find the center and the radius