Solve
-If the Three Lengths of the Sides of a Triangle

Multiple Choice

Solve.
-If the three lengths of the sides of a triangle are known, Heron's formula can be used to find its area. and $c$ are the three lengths of the sides, Heron's formula for area is:
$$A = \sqrt { s ( s - a ) ( s - b ) ( s - c ) }$$
where $s$ is half the perimeter of the triangle, or $s = \frac { 1 } { 2 } ( a + b + c )$ .
Use this formula to find the area of the triangle if $a 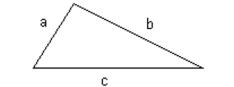= 9 \mathrm {~cm} , \mathrm {~b} = 11 \mathrm {~cm}$ and $c = 16 \mathrm {~cm}$ .

A) $3 \sqrt { 14 } \mathrm { sq } \mathrm { cm }$
B) $18 \sqrt { 7 } \mathrm { sq } \mathrm { cm }$
C) $18 \sqrt { 14 } \mathrm { sq } \mathrm { cm }$
D) $180 \sqrt { 15 } \mathrm { sq } \mathrm { cm }$ , b,