Multiple Choice
Graph using the slope and the y-intercept.
- 
A) 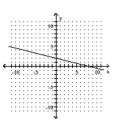
B) 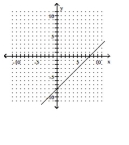
C) 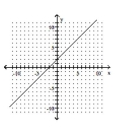
D) 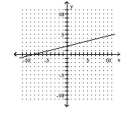
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q39: Graph.<br>-y + 3 = 0 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6465/.jpg"
Q40: Solve.<br>-The height h in feet of a
Q41: Determine the slope and the y-intercept.<br>-f(x)= -8x
Q42: Tell whether the lines are "parallel",
Q45: Find a linear function whose graph
Q46: Find the domain.<br>- <span class="ql-formula" data-value="f
Q47: Find the slope of the line
Q48: Solve the problem.<br>-The function <span
Q49: Find a linear function whose graph
Q306: Explain why the order in which coordinates