Multiple Choice
Solve using the addition principle. Graph and write set-builder notation for the answer.
- 
A) 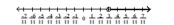
B) 
C) 
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q53: Solve using the multiplication principle.<br>- <span
Q54: Solve using the addition principle. Graph
Q55: Solve the problem. Round to the nearest
Q56: Solve. Clear fractions first.<br>- <span class="ql-formula"
Q57: Translate the sentence to an inequality.<br>-A
Q59: Solve using the multiplication principle.<br>--9.9y =
Q60: Solve.<br>- <span class="ql-formula" data-value="4 k +
Q61: Solve the problem.<br>-At the end of the
Q62: Translate the sentence to an inequality.<br>-The
Q63: Determine whether the given number is