Multiple Choice
Solve the problem.
-The half-life of Antimony 111 is hours. If the formula gives the percent (as a decimal) remaining after time (in hours) , sketch P versus .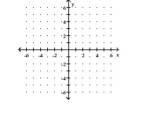
A) 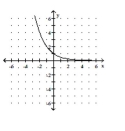
B) 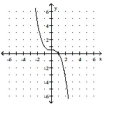
C) 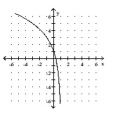
D) 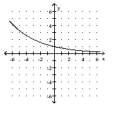
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q16: Use composition to verify whether or
Q17: Find f(x) and g(x) such that
Q18: Determine whether the function is one-to-one.<br>-
Q19: Find f(x) and g(x) such that
Q20: Solve the problem.<br>-A size 38 dress
Q22: Find the inverse of the relation.<br>-{(6, -6),
Q23: Solve the problem.<br>-An accountant tabulated a
Q24: Determine whether the function is one-to-one.<br>-
Q25: Determine whether the function is one-to-one.<br>-
Q26: Graph the equation of the relation