Multiple Choice
Use the equation of the parabola in standard form to determine the coordinates of the vertex and the equation of the axis of symmetry (complete the square if necessary) . Then graph The parabola.
A) vertex: ;
Line of symmetry 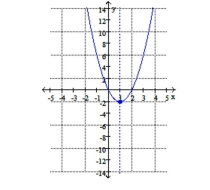
B) vertex: ;
Line of symmetry 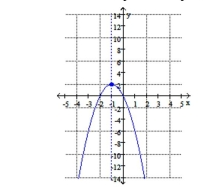
C) vertex: ;
Line of symmetry 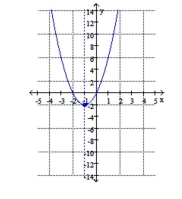
D) vertex: ;
Line of symmetry 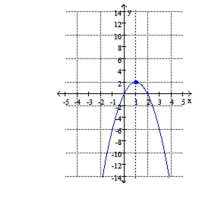
Correct Answer:

Verified
Correct Answer:
Verified
Q52: Identify the center and radius of
Q53: Find the midpoint of the line segment
Q54: Determine the vertex by using the
Q55: Which of the following is the
Q56: Solve the system of nonlinear equations
Q58: A map of a hiking area
Q59: Graph the solution set to the
Q60: Solve the system of nonlinear equations
Q61: Determine whether the transverse axis of
Q62: Graph the solution set. <span