Multiple Choice
Use the equation of the parabola in standard form to determine the coordinates of the vertex and the equation of the axis of symmetry (complete the square if necessary) . Then graph The parabola.
A) vertex ;
Line of symmetry 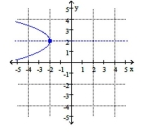
B) vertex ;
Line of symmetry 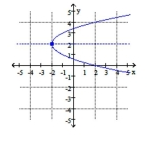
C) vertex ;
Line of symmetry 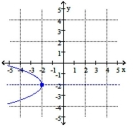
D) vertex ;
Line of symmetry 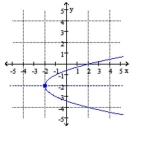
Correct Answer:

Verified
Correct Answer:
Verified
Q8: Sketch the system of equations. Then
Q9: Sketch the system of equations. Then
Q10: The point (5, 1) satisfies the
Q11: Describe the solution set for the
Q12: Describe the solution set for the
Q14: Solve the system of nonlinear equations
Q15: Use the equation of the parabola
Q16: Find the midpoint of the line segment
Q17: Determine the vertex by using the
Q18: Identify the center of the ellipse