The Following MINITAB Output Display Presents the Results of a Hypothesis

Multiple Choice

The following MINITAB output display presents the results of a hypothesis test for the difference $\mu _ { 1 } - \mu _ { 2 }$ between two population means.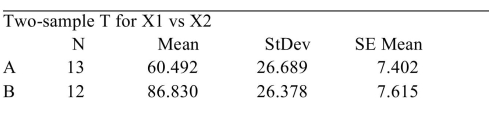

Difference $= \operatorname { mu } ( \mathrm { X } 1 ) - \operatorname { mu } ( \mathrm { X } 2 )$
Estimate for difference: $- 26.338$
$95 \%$ CI for difference: $( - 47.152 , - 5.524 )$
$\mathrm { T }$ -Test of difference $= 0 ($ vs not $= ) :$ T-Value $= - 2.480133$
$\mathrm { P } -$ Value $= 1.979112 \quad \mathrm { DF } = 23$
How many degrees of freedom are there for the test statistic?

A) 22
B) 26.338
C) 23
D) 1.979112