Multiple Choice
Sketch the graph of the function. Describe how the graph can be obtained from the graph of a basic logarithmic function.
- 
A) Shift to the left 2 units,
stretch it vertically, and shift up 4 units 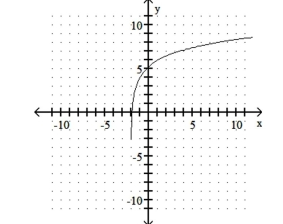
B) Shift to the right 2 units
,shrink it vertically, and shift up 4 units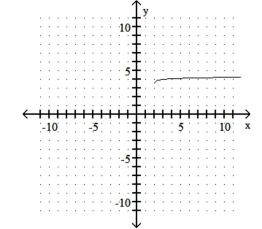
C) Shift to the left 2 units,
shrink it vertically, and shift down 4 units 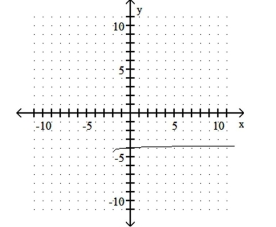
D) Shift to the left 2 units,
shrink it vertically, and shift up 4 units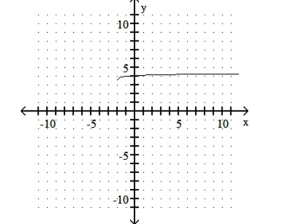
Correct Answer:

Verified
Correct Answer:
Verified
Q11: Solve.<br>-In 1998 , the population of
Q12: For the function f, use composition
Q13: Provide an appropriate response.<br>-Prove that the
Q14: Provide an appropriate response.<br>-Explain the error
Q15: Solve the logarithmic equation.<br>- <span class="ql-formula"
Q17: Solve the problem.<br>-Suppose the amount of
Q18: Solve the logarithmic equation.<br>- <span class="ql-formula"
Q19: Choose the function that might be
Q20: For the function f, use composition
Q21: Solve the exponential equation. Round to